예전에 AVL tree를 보고 나서 RB tree를 봐야지! 했는데 어쩌다보니 B-tree를 먼저 보게 되었네요.... 자료구조 수업에 따라 B-tree까지 배울 수도 있다고 하는데, 제 학부 수업을 생각하면 학부 수업때 어떻게 여기까지 나갈 수 있나 싶습니다. 정말 복잡하고 심오한 자료구조인 만큼 배우는 사람도 적은 것 같고, 한글로 된 자료가 비교적 적기도 합니다.
복잡한 자료구조다보니 틀린 부분이 있을 수 있습니다. 실제로 구글링 시 뜨는 한글 자료 중 오류를 범한 자료가 있기도 하구요. 틀린 부분이 있다면 댓글 달아주시면 확인하고, 수정하도록 하겠습니다.
한글, 영어 상관 없이 각 자료에서 사용하는 용어들이 조금씩 다른 의미를 가지고 있습니다. B-tree 영문 위키에도 'Differences in terminology'라는 소제목으로 논문마저도 용어들이 다른 뜻을 가질 수 있다고 합니다. 여기서는 지금 정의하는 minimum degree, order, leaf를 사용할 것입니다.
Minimum degree $t$: Node가 가질 수 있는 최소 child의 수, $t \ge 2$
Degree, Order: Node가 가질 수 있는 최대 child의 수
Leaf: Lowest level of keys. Key값이 저장된 가장 깊은 depth의 node들을 의미
본 포스팅을 작성하면서 참고한 자료들은 다음과 같습니다. 기본적으로 CLRS를 공부하면서 다양한 자료들을 찾아보았습니다.
Introduction to Algorithm(이하 CLRS, Chap 18. B-trees)
CLRS Chap.18 Solution(for pseudocode of deletion)
영문 Wikipedia(B-tree)
C로 쓴 자료구조론(Chap 11. 다원 탐색 트리)
GeeksforGeeks(Introduction, Insert)
백인감자 블로그
guru99
B-tree 시각화 사이트
1. B-tree의 정의
B-tree T는 다음과 같은 성질을 가지고 있습니다.
1. 모든 node $x$는 다음 attribute를 가지고 있습니다.
- $x.n$: Node $x$에 저장된 key의 갯수
- $x.key_{1} \le x.key_{2} \le \ ... \ \le x.key_{x.n}$: Node 내의 key들은 오름차순으로 정렬되어 있습니다.
- $x.leaf$: True일 경우 node $x$는 T의 leaf, False일 경우 internal 또는 root node
Leaf node의 정의는 저 위에서 했고, root node는 B-tree T의 root, 그 외 나머지 node들을 internal node라고 합니다.
2. 각 internal node $x$는 $x.n+1$개의 pointer를 가집니다.
- 각각 $x.c_{1}, x.c_{2}, \ ... \ x.c_{n+1}$ child를 가리킵니다.
- Leaf node는 child가 없습니다.(구현에 따라 다를 수 있습니다)
3. $x.key_{i}$는 각 (위에서 언급한 child를 root로 하는)subtree에 저장된 key들의 범위를 나누는 역할 또한 수행합니다.
- $k_{i}$를 $x.c_{i}$를 root로 하는 subtree에 저장된 any key라 하면 다음과 같은 관계가 성립합니다.
- $k_{1} \le x.key_{1} \le k_{2} \le \ ... \ \le x.key_{x.n} \le k_{x.n+1}$
4. 모든 leaf는 B-tree T의 height을 depth로 가집니다. 즉, 모든 leaf의 depth는 같습니다.
5. 모든 node는 가질 수 있는 최소/최대 key 갯수가 정해져 있습니다.
- 위에서 정의한 2 이상인 minimum degree $t$는 node가 가질 수 있는 최소 child의 수입니다.
- $t$개를 나누는 칸막이는 $t-1$개가 필요하니 모든 internal node는 최소 $t-1$개의 key를 가지고 있어야 합니다.
- 예외적으로 root node는 1개 이상의 key만 가지고 있으면 됩니다.
- Root node가 empty인 경우, empty tree T가 아닌 이상 root의 child는 1개 있으므로 height를 낮추면 됩니다.
- 모든 node는 최대 $2t-1$개의 key를 가질 수 있습니다.
- 왜 $2t-1$개인지는 insert, delete 연산을 수행하다보면 알 수 있습니다.
Node가 $t-1$개 key를 가지고 있는 경우를 minimum node, $2t-1$개 key를 가지고 있는 경우를 full node라고 지칭하겠습니다.
Minimum degree $t$의 최솟값은 2인데, $t=1$인 경우는 그냥 BST가 되어버리기 때문인 것 같습니다. 조건이 꽤 복잡한데, 이런 B-tree T의 height는 어떻게 될까요? Worst case를 보도록 합시다.
Root는 1개의 key를 가지고, 나머지 node들은 최소인 $t-1$개의 key만을 가진다고 합시다. 이 때 depth에 따른 node 갯수는 다음과 같습니다.
| Depth | 1 | 2 | 3 | ... | h |
| Node 갯수 | $2$ | $2t$ | $2t^{2}$ | ... | $2t^{h-1}$ |
B-tree T에 저장된 총 key 갯수를 $n$이라 하면, 다음과 같은 등식이 성립합니다.
$n \ge 1 + (t-1)\sum_{i=1}^{h}2t^{i-1} = 1 + 2(t-1)\cdot\frac{1\cdot(t^{h}-1)}{t-1} = 2t^{h}-1$
2번째 항의 1은 root node의 key 개수, $\sum$ 앞에 붙은 $t-1$은 각 노드에 저장되는 key의 개수입니다. 위 식을 잘 풀면 $\ t^{h} \le \frac{n+1}{2}$이므로, $\ h \le log_{t}\frac{n+1}{2}$임을 보장할 수 있습니다. 각 노드에 최소 갯수의 key를 저장한다고 해도 B-tree의 height이 $O(log_{t}n)$으로 억제될 수 있음을 확인할 수 있습니다.
2. B-tree의 search operation
Insert, delete에 비해 비교적 간단한 search operation부터 봅시다. 현재 보고 있는 internal node $x$에 저장된 key의 갯수는 $x.n$이므로 ($x.n+1$)-way decision이 가능합니다. Root node의 pointer와 찾고자 하는 key k를 input으로 넣으면, k가 있다면 해당 node와 index를 return하고, 없으면 Null을 return하면 됩니다.
모든 node에 저장된 key값은 오름차순으로 정렬되어 있으므로, $k \le x.key_{i}$를 만족하는 가장 작은 $i$를 찾고, $k$값과 $x.key_{i}$이 같으면 ($x, i$)를 return, 같지 않고 $x$가 leaf node면 Null을 return(k가 없음), 같지 않고 $x$가 leaf node가 아니면 재귀적으로 탐색을 수행하면 됩니다. 위에서도 언급했지만, internal node의 key는 key값 그 자체로서의 의미도 있지만 subtree의 key 범위를 나누는 역할 또한 수행합니다.
3. B-tree의 insert operation
AVL tree에서는 insert 수행 후 AVL tree의 조건(High-Balance Property)을 만족하게 하기 위해 상황에 따라 4가지 rotation을 수행했습니다. 마찬가지로 B-tree에서도 full node($x.n = 2t-1$)에 새로운 key를 추가하게 될 경우 B-tree의 조건이 깨지게 되므로 적절한 조치를 취해야 합니다. 여기서는 "split"을 통해 full node를 2개의 node로 나누고, insert를 수행하게 됩니다. 다음 그림은 CLRS 책에서 소개하는 split 예시 그림입니다.

Node $y$의 median인 $S$가 parent node인 $x$로 올라가고, $S$를 기준으로 양 쪽의 ($P, Q, R$), ($T, U, V$)가 각각 새로운 child가 되었습니다. Full node를 최소 size node인 $y, z$로 split할 수 있습니다. 뭐... 실제로 새로운 node 2개를 만드는 것은 아니고, 새로운 node $z$를 만들고 node $y$의 key 일부를 node $z$로 옮깁니다. CLRS에서 소개하는 split의 pseudocode는 다음과 같습니다.

Fig 18.5에서 key값들의 대소 비교를 해보면 $N \le (P,Q,R) \le S \le (T,U,V) \le W$입니다. Full node $y$를 split하면 $y$의 parent node인 $x$의 key는 1개 늘어나고($y$의 median key), 남은 $y$의 key들은 $x$로 올라간 key를 기준으로 2개의 minimum node로 split됩니다. 앞서 node가 가질 수 있는 최대 key 갯수가 $2t-1$이라고 했었는데, 그렇게 정의해야 full node를 split하면 2개의 minimum node로 split될 수 있기 때문이라고 생각합니다. Split 함수에서 아래로 가지를 치지 않고 위로 key를 보내는 이유는, 그래야지 특정 leaf의 depth가 다른 leaf보다 커지는 것을 방지하기 때문입니다. 이 부분은 포스팅의 마지막 부분에서 다시 언급하게 될 것 같습니다.
Node $y$가 full node여서 split을 진행했는데 만약 $x$ 또한 split 이전 full node인 경우에는 어떻게 하냐구요? 그럴 일은 없습니다. Node $x$가 full node였으면 $x$의 parent node에서 먼저 $x$에 대해 split을 진행했을 것입니다. 따라서 split을 반복하기 위해 parent로 돌아가는 일은 일어나지 않습니다.
Split 함수의 시간복잡도는 $O(t)$입니다. $y$의 뒷부분을 $z$에 복사하는 것과, $S$를 $x.key_{i}$에, $z$을 $x.c_{i+1}$에 넣기 위해 기존 key, child를 뒤로 미는데 각각 $O(t)$만큼 소요됩니다.
Full node에 insert하는 데 필요한 선행 작업인 split을 봤으니, 이제 non-full node에 insert하는 pseudocode를 보도록 합시다. 새로운 key k는 무조건 leaf node에 insert됩니다. 왜 그런지는 포스팅의 마지막 부분에서 생각해봅시다.

Root node가 아닌 node $x$에 새로운 key k를 insert하는 pseudocode입니다. 크게 line 2-8, line 9-17 두 부분으로 나눌 수 있습니다.
우선 line 9-17은 현재 탐색하고 있는 node $x$가 internal node여서 어느 child에 k가 들어갈 지 결정하는 부분입니다. search와 마찬가지로 어느 범위 내의 subtree에 k가 들어갈 지 찾고 재귀적으로 insert-nonfull 함수를 수행합니다. 주의할 점은, k가 들어가야 하는 child가 full node인 경우, 해당 child 탐색 이전에 먼저 split을 수행하고 탐색을 한다는 것입니다.
왜 이렇게 하냐구요? 단순히 k가 들어가야 하는 leaf를 찾고 insert를 먼저 해도 되지만, 그 leaf이 full node였을 경우에는 다시 parent로 되돌아가면서 split을 수행해야 합니다. Leaf node를 split해서 key 하나를 parent로 올렸는데 그 parent 또한 full node였다면? 또 split을 하고 그 위로 돌아가야 하구요. 이렇게 parent node로 되돌아 가는 것을 CLRS에서는 "back up"이라고 표현합니다. Back up을 하게 되는 경우 기존 downward path를 모두 기억하고 있어야 parent node로 돌아갈 수 있습니다. CLRS에서는 back up 과정을 최대한 줄이고 “one-pass downward operation"을 수행하기 위해 위와 같이 먼저 split을 진행합니다. 나중에 볼 delete에서도 back up을 최대한 줄이기 위해 영문 위키, 여타 자료들과는 다른 방식으로 pseudocode를 만들었습니다. 스포일러 조금 하자면, insert에서는 back up이 일어나지 않지만, delete에서는 어쩔 수 없이 back up을 해야 하는 경우가 생깁니다. 그래도 back up을 여러번 하는 것이 아니라 딱 한 번 합니다. 그 back up을 하기 위해 downward path를 기억할 필요도 없구요.
아무튼, child가 full node인 경우 선제 split을 수행하기 때문에, 현재 탐색하는 node $x$가 leaf인 경우인 line 2-8의 경우 $x$가 full node인지 확인 할 필요 없이 바로 k를 집어넣으면 됩니다. 따로 Back up을 할 필요도 없구요.

이제 insert를 위해 B-tree T와 새로운 key k를 input으로 받는 함수입니다. Root node가 full node인 경우에는 median key를 올릴 parent node가 존재하지 않습니다. 따라서 새로운 root node $s$를 만들고, 기존 root node였던 $r$을 node $s$의 첫 번째 child로 만든 후 위에서 본 split 함수를 수행하면 됩니다. Root node가 full node가 아닌 경우에는 바로 insert-nonfull 함수를 수행하면 됩니다.
Insert operation의 시간 복잡도는 $O(log_{t}n)$이라고 합니다. 결국 leaf node에 insert되기 때문에 height에 영향을 받는데, 저는 처음에 "$O(t\cdot log_{t}n)$이 왜 아닐까"라고 생각했었습니다. 이유는, $t$가 constant이기 때문에.... 사라지는게 당연한 것이었어요...
Insert operation을 공부하면서 생긴 궁금증, (맞는지는 모르겠지만)깨달은 것들이 있습니다. 우선 delete operation까지 보고 한꺼번에 고찰해보도록 합시다.
4. B-tree의 delete operation
Insert도 복잡하다고 생각했는데, delete는 더더욱 복잡합니다. 심지어 여러 자료들이 제각각 설명하는 방식이 달라서 많이 헷갈렸습니다. Delete를 몇 가지 case로 나눌 수 있는데 저는 CLRS에서 제시한 방법을 먼저 따라가고, 여러 자료에서 제시한 case가 CLRS에서 어떤 경우에 부합하는지 보도록 하겠습니다.
Insert에서는 full node에 insert하여 maximum key 갯수 조건을 깨는 것을 방지하기 위해 split이라는 방법을 사용했습니다. 비슷하게 delete에서는 minimum node에서 delete를 하는 것(underflow)을 방지하기 위해 merge, rotate를 사용합니다.
또한 leaf node의 key를 지우는 것은 괜찮은데, internal node의 key를 지우게 되는 경우에는 해당 key에 의해 구분되는 child(subtree)까지 손을 봐야합니다. 그래서 복잡하니, CLRS에서 제시하는 방법을 따라 차근차근 공부해봅시다. B-tree T에서 key k를 삭제한다고 합시다. 이 때 최초 delete 함수의 input은 T의 root node와 key k입니다. 현재 보고 있는 node가 $x$라고 할 때 나올 수 있는 여러가지 경우들에 대해 알아봅시다.
1. Node $x$에 key k가 있고, $x$가 leaf node인 경우
간단하게 k를 삭제하면 됩니다. Leaf node가 minimum node일수도 있지 않냐구요? 그럴 일은 절대 없으니 걱정 안 하셔도 됩니다. 삭제하고자 하는 key k를 포함하는 leaf node $x$가 minimum node가 되지 않도록 나중에 볼 3번 단계에서 '미리' 처리합니다. 앞서 설명한 back up을 최대한 방지하기 위해 '미리' 무언가를 처리하고, 이게 다른 자료, 영문 위키에서 소개하는 delete operation과의 차이점입니다.
2. Node $x$에 key k가 있고, $x$가 leaf node가 아닌 경우(3가지 case)

위 그림을 기반으로 3가지 case를 봅시다. Child node인 $y$, $z$의 key 갯수에 따라 나눠집니다. 첫 두 가지 case는 쉽게 생각해보면 삭제하고자 하는 key k를 적당한 leaf로 보내 삭제하고, 기존 k 위치에는 k 역할(subtree의 key 범위를 나누는)을 할 수 있는 적당한 key를 가져온다고 볼 수 있습니다.(실제 작동 방식은 조금 다릅니다)
2-1 k의 left child node $y$가 t개 이상의 key를 가지는 경우

Key k가 $x.key_{i}$일 때 $x.c_{i}$를 root로 하는 subtree에서 가장 큰 key값인 $k^{'}$을 찾습니다.(Inorder traversal 시 k의 predecessor 역할을 하는 key입니다) 그림에서 $k^{'}$의 위치가 잘못 되었는데, B-tree 성질에 따라 $y$를 root로 하는 subtree의 가장 오른쪽 leaf의 가장 마지막 key입니다. $x.key_{i}$를 $k^{'}$로 대체하고, $y$와 $k^{'}$를 input으로 하는 delete 함수를 수행합니다.
2-2 k의 left child node $y$가 t-1개 key를 가지고, right child node $z$가 t개 이상의 key를 가지는 경우

Case 2-1과 symmetric하게, $x.c_{i+1}$을 root로 하는 subtree에서 가장 작은 key값인 $k^{'}$을 찾습니다.(Inorder traversal 시 k의 successor 역할을 하는 key입니다) 위와 같이 $x.key_{i}$를 $k^{'}$로 대체하고, $z$와 $k^{'}$를 input으로 하는 delete 함수를 수행합니다.
2-1, 2-2의 경우 k의 predecessor/successor를 찾고 다시 node $x$로 돌아와야 하는데, 이 것이 앞서 이야기한 delete에서 발생하는 불가피한, 유일한 back up입니다.
2-3 k의 left child node $y$, right child node $z$가 모두 t-1개 key를 가지는 경우
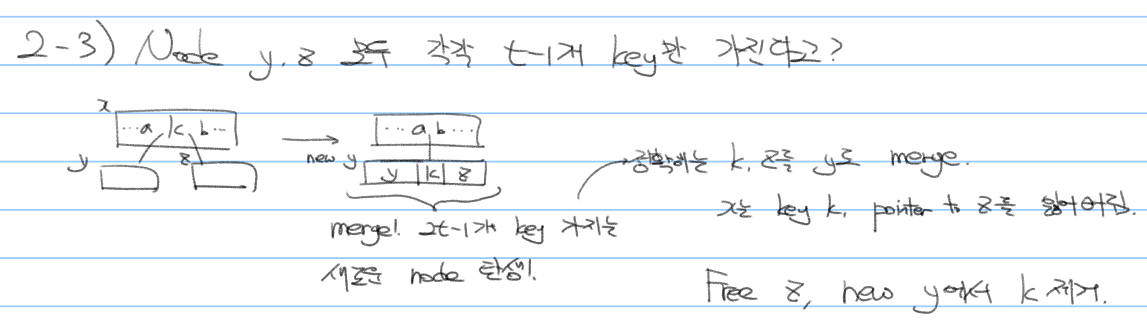
이 경우에는 특별히 $x.key_{i-1} = a$, $x.key_{i+1} = b$를 고려해야 합니다. 2개의 minimum child node($y$, $z$)와 삭제하고자 하는 key k를 하나의 node로 merge하고, k를 지워 새로운 $2t-2$개의 key를 가지는 node를 만들어줍니다. 이 node 내 모든 key는 $a$보다는 크고 $b$보다는 작으니 위 그림과 같이 $a$와 $b$ 사이의 child로 assign할 수 있습니다. 편의상 new y라고 적었는데, 사실은 기존 node $y$에 $z$를 붙이고 기존 $z$를 날려버리면 됩니다.
여기서 '$y$, $z$의 key 갯수과 상관 없이 case 2-1, 2-2를 수행할 수 있지 않은가?'라고 생각할 수도 있는데, 만약 $y$, $z$가 모두 leaf node이고 $t-1$개 key를 가진다고 생각해봅시다. Merge하지 않고 predecessor/successor를 찾아 k를 대체하고 $y$/$z$와 predecessor/successor를 input으로 하는 delete 함수를 수행하면? $y$, $z$ 모두 leaf node이면서 지우고자 하는 key를 가지고 있기 때문에 1번 경우에 해당하고, 이 node가 minimum node인지 확인하지 않고 key를 삭제하는 불상사가 발생해버립니다. 그래서 case 2-3의 경우 merge를 해 줘야 합니다.
이제 마지막 case로 넘어가봅시다.
3. Node $x$에 key k가 없는 경우(3가지 case)
현재 보고 있는 node에 삭제하고자 하는 key가 없기 때문에, 어느 child에 k가 있을 지 탐색해서 해당 child node와 k를 input으로 하는 delete 함수를 재귀적으로 실행해야 합니다. $x.c_{i}$를 root로 하는 subtree에 key k가 있다는 사실을 확인했다고 합시다.
3-0) $x.c_{i}$가 t개 이상의 key를 가지고 있는 경우
별 다른 조치 없이 recurrsive하게 delete 함수를 수행하면 됩니다.
3-1) $x.c_{i}$가 t-1개 key를 가지고 있으면서, immediate sibling(인접 child)이 t개 이상의 key를 가지고 있는 경우

대부분의 자료에서 "rotate"라고 지칭하는 경우입니다. 여기서는 $t=3$이고, $x.c_{i}$에 k가 있으면서 2개의 key를 가지고 있고, 오른쪽 sibling인 $x.c_{i+1}$이 t개 이상의 key를 가지고 있는 경우를 봅시다. 우리의 목표는 $x.c_{i}$가 minimum node가 되지 않도록 하는 것입니다.
포스팅 초기에 subtree의 any key와 key값 간 크기 비교했던 것을 돌이켜보면 위 그림으로부터 다음과 같은 관계가 있다고 생각할 수 있습니다.
$... \le c \le \ ... \ e \le key(3) \le a \le key(4) \le f \le ...$
그러면, $x.key_{i} = a$를 $x.c_{i}$의 새로운 key로 옮기고, 그에 따라 존재해야 하는 $x.c_{i}$의 4번째 child는 그림에서 $x.c_{i+1}$의 첫 번째 child인 4를 가져오며, 그에 따라 필요가 없어진 $x.c_{i+1}$의 첫 번째 key f를 (a가 사라져서)비어있는 $x.key_{i}$ 자리에 넣어주면 $x.c_{i}$가 더 이상 minimum node가 아니라는 목표를 달성하면서 B-tree의 조건 또한 모두 충족할 수 있습니다.
3-2) $x.c_{i}$가 t-1개 key를 가지고 있으면서, immediate sibling(인접 child) 또한 t-1개 key를 가지고 있는 경우

이제는 immediate sibling 모두 t-1개 key만을 가지고 있기 때문에, immediate sibling으로부터 key 하나를 뺏는 행위가 불가능합니다. 그렇다면? case 2-3에서 본 merge를 여기서 사용하면 됩니다. 여기서도 우리의 목표는 $x.c_{i}$가 minimum node가 되지 않도록 하는 것입니다. 이번에는 삭제되는 key가 없기 때문에 merge되어 만들어진 node $x.c_{i}$는 full node입니다.
이번에도 $x.c_{i}$와 오른쪽 sibling인 $x.c_{i+1}$을 조작하는 경우를 봅시다. 간단하게, $x.c_{i}$에 $x.key_{i}$, $x.c_{i+1}$을 차례대로 이어 붙입니다. $x$ 입장에서는 갑자기 key 1개, child 1개가 사라졌기 때문에 $x.key_{i+1}$부터 끝까지 모든 key를, $x.c_{i+2}$부터 모든 child를 한 칸씩 땡겨주면 됩니다. 결과적으로 $x$의 key가 1개 줄어드는 대신 $x.c_{i}$가 minimum node가 되지 않도록 하는 목적은 달성했습니다.
$x$의 key가 줄어들었으니, $x$가 internal node일 때, root node일 때를 각각 생각해봅시다. 우선 $x$가 internal node이면 $x$의 parent node에서 이미 3번 과정을 수행했기 때문에 $x$는 최소 t개 이상의 key를 가지고 있음이 보장됩니다. $x$가 root node인 경우에는 root node는 1개 이상의 key만 가지고 있으면 되기 때문에 문제가 되지 않습니다. 만약 기존 root node $x$가 1개의 key만 가지고 있었다면? $x.c_{1}$과 $x.key_{1}$, $x.c_{2}$를 merge해서 만든 full node $x.c_{1}$을 B-tree의 새로운 root로 삼으면 해결됩니다. 이 경우 B-tree의 height이 1 감소하겠네요.(CLRS Fig 18.8 e' case)
Case 3의 일련의 과정을 통해 k가 있을 것이라고 생각되는 child의 key 갯수를 무조건 t개 이상으로 만들기 때문에, case 1에서 leaf node에 k가 있는 경우 걱정 없이 바로 삭제해도 되는 것입니다. Delete operation의 pseudocode는 참고자료의 CLRS Chap.18 Solution에 있습니다. 아마 저 pseudocode도 너무 길어서 일부를 생략한 것으로 알고 있습니다.
번외. 다른 자료들의 delete는 어떠한가?
우선 영문 위키피디아의 B-tree(Deletion) 항목을 보면, two popular strategies for deletion from a B-tree가 있다고 소개하면서 1번으로는 일단 delete하고 rebalance(restructure)하는 것, 2번으로는 CLRS처럼 delete하기 전에 restructure하는 것이 있다고 소개합니다. 이후의 과정은 1번 strategy를 따라가는 것 같습니다. 미리 restructure를 하는 과정이 없기 때문에 internal node에서 delete가 일어나는 경우 case 2-3이 존재하지 않습니다.
백인감자님의 블로그의 경우, internal node에서 delete가 일어나는 경우는 CLRS와 같지만 leaf node에서 delete가 일어나는 경우에 영문 위키처럼 사후 restructure를 수행합니다. CLRS에서는 case 3을 통해 사전 restructure를 수행해 leaf node에서 delete가 일어날 때 leaf node는 무조건 minimum node가 아니도록 강제합니다.
5. B-tree에 대한 고찰
*컴퓨터 관련 수업이라고는 학부 자료구조, 알고리즘밖에 안 들은 상태라 얕은 지식으로 인한 틀린 내용이 있을 수 있습니다.
1. BST와 다른 점?
- Node 갯수를 줄일 수 있다. 또한, tree의 height이 $O(log_{2}n)$에서 $O(log_{t}n)$으로 감소한다.
- 그래서 node를 읽는 횟수(pseudocode에서 DISK-READ)를 줄일 수 있다.
- 좀 깊게 들어가서, B-tree는 필요한 node(page)만 main memory에 올려 읽으면 된다.
- Root node를 기본적으로 main memory에 올려두고, 탐색 과정에서 node 읽는 횟수를 최소화

- CLRS 487페이지 하단, 그리고 geeksforgeeks 질문글에 따르면 B-tree의 시간복잡도는 disk I/O에 영향을 받는다고 한다.
- 적당한 index $i$를 찾는 데 걸리는 시간은? Minimum degree t에 영향 받는데 어차피 constant니까 무시 가능!
- Disk I/O의 횟수가 곧 "number of nodes that loaded from disk to main memory"
2. 그럼 disk I/O 횟수를 최소화하려면 root 근처 node부터 꽉꽉 채워야 height이 줄어드는거 아닌가?
- Insert, delete 모두 각 node에 모든 key를 꽉꽉 채우지 않는다. 왜 그럴까?
- 앞서 증명한 B-tree height의 worst case: $\ h \le log_{t}\frac{n+1}{2}$
- 결국 B-tree의 height이 $O(log_{t}n)$으로 억제
- 영문 위키에 따르면 B-tree의 best case: $\ h \ge log_{2t-1}(n+1) -1$
- 모든 node가 full node인 경우, 이 때도 B-tree의 height은 $\Omega(log_{t}n)$
- 모든 node에 key를 꽉꽉 채워도 height에서 이점이 없음
- 모든 node를 full node 상태로 강제하지 않으면 operation 수행 시간 단축 가능
- 매 번 insert, delete 시 되도록 많은 node를 full node로 만들려면 더더욱 복잡한 작업이 필요할 것 같음
2-1. Root node 근처보다는 leaf node에 먼저 key가 쌓이는 것 같다. 왜 그럴까?
- 모든 leaf node의 depth를 통일시켜 어떤 key든 적당한 시간 내 찾을 수 있도록 B-tree 구조 유지
- Insert는 무조건 leaf node에, spilit은 대부분의 key는 2개의 minimum child에 저장
- Child node쪽이 parent node보다 많은 key를 가지고 있음
- B-tree height 증가는 root node의 split이 일어나면서 발생하는데 어차피 leaf node의 depth가 일정하게 유지된다면?
- Height 증가를 최대한 억제하는 것이 낫다! 그래야 시간 복잡도를 줄일 수 있으니까!
3. 왜 먼저 spilt, merge, rotate 등을 수행하는가?
- Back up을 최소화할 수 있기 때문
- Delete의 case 2-1, 2-2의 경우도 path를 모두 기억할 필요 없이 k가 존재하는 node $x$와 index만 기억하고 있으면 된다.
- 영문 위키처럼 먼저 insert, delete를 수행하게 되면 root부터 해당 key가 존재하는 곳까지의 path를 모두 기억하고 있어야 한다.
- 그래야 유사시(full node에 insert 또는 minimum node에서 delete) parent node로 올라가면서 조치를 할 수 있음
- 이 경우 이미 거쳐온 node를 또 read해야 하기 때문에 시간적으로 손해
- 메모리 절약 가능!
'다양한 이야기 > 자료구조' 카테고리의 다른 글
| [자료구조] AVL tree (0) | 2020.08.27 |
|---|
