Additional Item and List-Based Metrics
강의 링크 : https://www.coursera.org/learn/recommender-metrics/home/welcome
Coursera | Online Courses & Credentials From Top Educators. Join for Free | Coursera
Learn online and earn valuable credentials from top universities like Yale, Michigan, Stanford, and leading companies like Google and IBM. Join Coursera for free and transform your career with degrees, certificates, Specializations, & MOOCs in data science
www.coursera.org
이전 게시글에서 다룬 metric들은 모두 data를 train, test set으로 split하고 train set을 통해 학습시킨 후, hidden test set을 통해 모델을 평가하는 방식이었습니다. 예를 들어 user-item rating 정보를 10만개 가지고 있다면, 8만개를 이용해서 추천 시스템을 학습시키고 나머지 2만개로 잘 작동하는가를 확인할 수 있겠죠.
추천 시스템의 목적은 "아직 user가 알지 못하지만 좋아할 법한 item을 추천해주는 것"이라고 생각합니다. 하지만 앞서 언급한 metric들은 "이미 user가 좋아한다고 했지만 알려주지 않은 것들을 얼마나 잘 맞추는지"를 평가합니다. 본문에서는 다음과 같이 이야기합니다.
철수가 실수로 먹물을 엎질러 rating history의 일부가 훼손되었고, 이를 복원하는 것을 잘 한다고 해서 실제 서비스에서도 새로운 아이템을 잘 추천할 수 있을거라고 이야기할 수는 없습니다. 이전 게시글의 metric들은 user가 좋아하지만 숨기고 있던 것을 잘 예측하는지는 평가할 수 있지만, 평가하지 않은 새로운 item을 추천했을 때 user가 이를 얼마나 좋아할지는 예측할 수 없습니다. 최소한 offline evaluation에서 이를 알기는 쉽지 않겠죠.
그렇다면 이전에 언급한 metric이 모두 무용지물이냐하면 그건 또 아닙니다. 이러한 hidden data evaluation을 통해 진짜 성능이 좋지 않은 모델들을 걸러내고, 남은 model들을 이용해서 실제 서비스에 잘 적용시킬 수 있도록 resources를 절약할 수 있겠죠. 일부 훼손된 rating history마저 잘 복원시키지 못하는데 실제 서비스에서 잘 작동하는 것을 기대할 수는 없으니까요.
이번 글에서는 이전 게시글에서 나아가 추가적인 metrics에 대해 알아보도록 합시다. 이전 metric들은 실제 rating 점수를 얼마나 잘 예측했는지, 또는 good items를 얼마나 잘 추천했는지를 따졌다면, 이번에는 다른 관점에서 추천 시스템을 평가하는 metric을 알아봅시다.
1. Coverage
Coverage는 다양한 용도로 쓰일 수 있는 metric입니다. 간단하게는 전체 아이템 중 얼마나 추천 시스템이 추천할 수 있는지 퍼센트로 나타낼 수 있겠죠. 예를 들어, 마트에서 각 사람들에게 물건을 홍보하는 추천 시스템이 있는데, 거의 대부분의 사람들이 마트에서 빵을 사 간다는 것을 알고 모든 사람들에게 빵만 추천한다면 정확도야 높겠지만 쓸모가 없는 추천 시스템이 되겠죠.
실제로 다양한 diversity metric 중 aggregate diversity라는 이름의 metric이 있습니다. 다음과 같이 계산됩니다.
$ Diversity-in-top-N = |\bigcup_{u\in U} L_{N}(u)| $
$L_{N}(u)$는 user u에게 추천된 item list 중 상위 N개의 아이템을 의미합니다. 즉 위 metric은 모든 user에게 추천된 상위 N개의 중복되지 않은 item의 개수를 의미하죠. 추천 시스템이 만들어낼 수 있는 추천 아이템들이 얼마나 다양한지를 위 metric을 가지고 판단할 수 있습니다.
2. Popularity
두 번째로 볼 metric은 popularity입니다. 반대되는 말로는 novelty가 있습니다. 이 아이템의 popularity를 정의하는 방법은, 그 아이템의 평균 rating이나, 평점을 남긴 사람들의 수 등이 될 수 있습니다. 이러한 popularity가 높은 item이 많이 추천될수록 사람들은 비교적 익숙한 item을 많이 추천받게 될 것이고, 반대로 popularity가 낮은 item이 많이 추천될수록 생소한 item들이 추천될 것입니다.
3. Personalization
각 user에게 추천된 아이템이 얼마나 다른지를 통해 볼 수 있는 personalization입니다. 사람들에게 각각 추천된 top-N item이 얼마나 다른지를 볼 수도 있고, 모든 유저들에 대한 각 아이템의 variance of predictions를 구할 수도 있습니다.(사실 2번째 내용은 잘 이해가 가지 않습니다.) 이러한 personalization이 낮을수록 모든 user에게 비슷한 아이템들이 추천될 것이고, 높을 수록 user마다 다른 추천 아이템 리스트를 받아볼 가능성이 올라갑니다.
4. Serendipity
앞서 "생소한" 추천을 잠깐 언급했었는데, 이와 관련된 serendipity라는 용어도 있습니다. 사전적 의미는 "뜻밖의 재미"인데, 추천 시스템에서는 생각지도 못한 걸 추천 받았는데 만족도가 높은 경우를 떠올릴 수 있겠네요. 이 또한 많은 논문에서 다양한 계산 방법이 있다고 하는데, 강의에서 소개한 방법은 다음과 같습니다.
$ serend = \frac{1}{N} \sum_{i=1}^{N} max(Pr(s_{i} - Prim(s_{i}), 0) * isrel(s_{i}) $
어떤 user에게 추천된 top-N items에 대해 $Pr(s_{i})$는 예측한 점수, $Prim(s_{i})$는 "primitive estimate of obviousness", $isrel(s_{i})$는 실제 user와 item이 관계가 있는지를 나타내는(0, 1) 변수입니다. User-item 간 predict score에서 그 아이템이 얼마나 obvious한지를 빼고, 실제로 user-item이 관계가 있는지를 곱한 값을 사용합니다.
그러니까 user-item이 실제로 관계가 있다는 전제 하에, 덜 유명한 아이템이(낮은 Prim) 높은 예측 점수(높은 Pr)를 가질수록 해당 item의 점수가 올라갑니다. Item의 obviousness는 앞서 언급한 popularity 등을 사용할 수 있겠죠. 정말 "생소하지만 높은 만족도"라는 의미에 부합하는 계산 방식입니다.
저는 늘 듣는 몇 개의 음악만을 돌려 듣는 성향이 강한데 음원 스트리밍 서비스 쪽에서는 serendipity가 높은 음악, 그러니까 잘 듣지 않는 음악을 제게 추천해줄 수 있겠죠. 그러다가 만약 새로운 좋은 음악을 찾게 되면 해당 서비스를 더 많이 이용하게 될 것이구요.
5. Diversity
마지막으로 볼 내용은 diversity입니다. 본 강의에서는 추천 리스트 내에 얼마나 다양한 item이 들어있는가를 의미합니다. 제가 생각했던 diverse recommendation은 각 user에게 편향되지 않는, 다양한 추천 리스트를 만들어주는 것이었는데 여기서는 그 중 추천 리스트 내부의 다양성을 diversity라고 하는 것 같습니다.
강의에서도 나오는 diversity metric 중 하나로는 intra-list distance가 있습니다. 10개의 아이템이 들어있는 추천 리스트가 있다면, 모든 pairwise set을 만들어서(45개) 얼마나 비슷한지 유사도를 계산합니다. 유사도로는 영화라면 장르가 같은지, 음악이라면 가수가 같은지 체크할 수도 있고 다른 조건을 만들어서 jaccard similarity를 사용할 수도 있습니다[1]. Jaccard similarity가 얼마나 비슷한지를 나타내는 지표니까, 1을 뺀다던가 하는 식으로 similarity를 distance로 바꿔 사용합니다.
Intra-list distance는 list 내 순서와는 상관이 없습니다. 이전 글에서 NDCG라는, 리스트 내 추천 순서에 따라 accuracy를 평가하는 metric이 있다고 했었는데, diversity metric에서도 추천 순서에 따라 가중치를 두는 metric이 있습니다. 바로 $\alpha$-NDCG입니다.
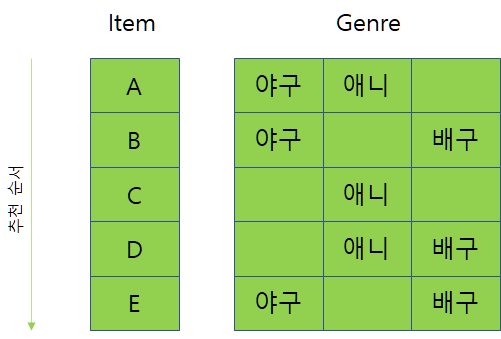
예시로, 5개의 영상을 추천받았다고 가정합시다. 영상의 주제는 총 3개이고, A라는 영상의 주제는 야구, 애니, E라는 영상의 주제는 야구, 배구입니다. 얼마나 다양한 주제의 영상이 리스트 내에 있는가를 diversity의 척도로 삼도록 하겠습니다. NDCG였다면 B라는 영상이 "정답인지 아닌지", 또는 "rating 점수"에 따라 B의 gain의 분자가 정해졌다면, a-NDCG에서는 "B의 주제인 야구, 배구가 이전에 얼마나 나왔는지"에 따라 분자가 정해집니다. a-NDCG의 gain은 다음과 같이 정해집니다.
$ G[k] = \sum_{i=1}^{m} J(d_{k}, i)(1 - \alpha)^{r_{i, k-1}} $
NDCG보다 조금 더 복잡한 것 같습니다. 우선 m은 주제의 총 개수입니다. J(d_{k}, i) 는 k번째 아이템 $ d_{k}$에 주제 i가 있으면 1, 없으면 0을 의미합니다. $\alpha$는 penalty를 의미하고, $r_{i, k-1}$은 k-1번째까지의 아이템 중 주제 i가 등장한 횟수입니다.
위 경우에 i=1이면 야구, i=2면 애니, i=3이면 배구라고 합시다. Penalty인 $\alpha = 0.5$라 하고, B(k=2)에 대해 G[k]를 계산해봅시다.
i=1인 경우, B는 야구라는 주제를 가지고 있으니까 $J(d_{2}, 1) = 1$이고, 앞서 야구라는 주제가 1번 등장했으므로 $r_{1, 1} = 1$이 됩니다.
i=2인 경우, B는 애니라는 주제를 가지고 있지 않으므로 $J(d_{2}, 2) = 0$입니다.
i=1인 경우, B는 배구라는 주제를 가지고 있으니까 $J(d_{2}, 3) = 1$이고, 앞서 배구라는 주제가 0번 등장했으므로 $r_{3, 1} = 0$이 됩니다.
그럼, G[2] = 0.5 + 0 + 1이 되어 B는 1.5점이라는 gain을 가지게 됩니다. 각 주제에 대해 이전에 적게 등장할수록 더 많은 점수를 얻을 수 있다는 것을 확인할 수 있습니다. A~E에 대해 G[]를 계산해보면 다음과 같습니다.
G[1] = 1 + 1 + 0
G[2] = 0.5 + 0 + 1
G[3] = 0 + 0.5 + 0
G[4] = 0 + 0.25 + 0.5
G[5] = 0.25 + 0 + 0.25
이후 DCG, IDCG를 구해 $\alpha$-NDCG를 구하는 부분까지는 NDCG와 같습니다. 정답이 추천 리스트 앞쪽에 모여 있을수록 점수가 더 높은 NDCG처럼, 다양한 장르를 가진(겹치지 않는) item들이 앞쪽에 모여 있으면 더 높은 점수를 받을 수 있습니다. 개인적으로 궁금한 것은 penalty인 $\alpha$의 역할인데, 아무래도 다양한 주제를 많이 가진 item일수록 G[]값아 높아질 가능성이 크니까 이를 제한하는 것인가 하는 생각이 드네요. 조금 더 공부해봐야겠습니다. 레퍼런스로 처음 이 metric을 보고 공부한 논문을 걸어둡니다[2].
Diverse한 추천 list를 만드는 방법으로 Cai Ziegler의 topic diversification in recommender systems에 관한 논문[3]과 bundling이라는 방법을 소개합니다. 제가 공부하면서 읽었던 논문들은 나아가서 강화학습을 쓰기도 하고, GAN을 쓰기도 하고, GNN을 사용하기도 하더라구요. 제가 알고 있었던 "다양한 종류의 item을 user에게 추천하는 것"을 diversity라고 한다면, diversity를 높일수록 비교적 accuracy(NDCG 등)은 떨어질 수밖에 없습니다.
제가 야구와 애니메이션을 좋아한다고 해서 유튜브 메인 화면에 야구, 애니 동영상만 주루룩 띄워놓으면 정확도야 올라가지만 유튜브에 대한 제 만족도는 바닥을 치겠죠. 하지만 축구도 띄워주고, 전자기기 영상도 띄워주고 하면 정확도는 조금 떨어질 수 있어도 앞서 언급한 serendipity를 찾으면서 만족도는 올라갈 수도 있겠죠. 실제로 구글에서 낸 diverse recommendation 논문[4]에서는 이러한 추천을 통해 homepage 영상을 바꾼 것만으로 homepage 영상 시청 시간 증가, 해당 영상으로부터 related video activity 증가 등의 효과를 이끌어냈다고 합니다. 이거 읽으면서 DPP라던가 논문 정리를 했었는데 어디갔는지.... 다시 블로그에 정리해야겠네요.
이번 글에서 본 metric들은 accuracy와는 거리가 살짝 있는 metric입니다. 경험 상 diversity를 올리기 위해 accuracy를 조금 희생하는 경우가 많았습니다. 논문들의 experiment 부분을 보면 물론 둘 다 올린 경우도 있지만, 이전 논문들에 비해 더 적은 accuracy 하락과 더 큰 diversity 증가를 이끌어냈다고 한 논문들이 많았던 것으로 기억합니다. 이러한 움직임이 실제 서비스에서 유저들의 만족도를 높이는데 도움이 된다면, 약간의 accuracy 희생은 충분히 합리적이라고 생각할 수 있겠죠.
여담으로 이번에는 latex 문법 적용이 딱 한 부분 빼고 잘 되네요. 다행입니다. 혹시라도 틀린 부분이 있으면 지적 부탁드립니다.
Reference
[1] Y. Liu et al, “Diversitypromoting deep reinforcement learning for interactive recommendation,” arXiv preprint, 2019.
[2] C. Clarke et al, "Novelty and Diversity in Information Retrieval Evaluation", SIGIR, Jul. 2008.
[3] C. Ziegler et al, "Improving Recommendation Lists Through Topic Diversification", WWW, May. 2005.
[4] M. Wilhelm et al, "Practical Diversified Recommendations on YouTube with Determinantal Point Processes", CIKM, Oct. 2018.
'추천 시스템 > Coursera' 카테고리의 다른 글
| Evaluation and Metrics - Online Evaluation (0) | 2020.09.11 |
|---|---|
| Evaluation and Metrics - Unary data (0) | 2020.08.17 |
| Evaluation and Metrics - Experimental Protocols (0) | 2020.08.14 |
| Evaluation and Metrics - Basic metrics (0) | 2020.08.07 |

